This post describes a variation of the algorithm Relational Perspective Map (RPM)[1]. The new algorithm, called generalized RPM (gRPM), is more sound from the view point of simulated dynamical system; and produces in general more consistent maps. gRPM has been implemented in VisuMap and has been available since version 2.4. In the following I'll first review the RPM algorithm; then describe gRPM for a special case that employs flat torus topology; I'll then discuss possible variation and extension of the algorithm.
As a MDS (multidimensional scaling) algorithm, RPM seeks to map a set of data points from high dimensional space to the surface of a torus, so that the following "Energy" is minimal:
where δij is the distance matrix between the data points in the high dimensional space; and dij is the distance matrix for the data points on the torus. RPM uses the gradient-descent algorithm to minimize the energy E, so that RPM in effect simulates a multi-particle system to find a minimal energy configuration on the torus directed by the following "force":
The negative sign in above formula indicates that the "particles" exert repulsive force on each other; and the closer two "particles" are on the torus, the larger is the repulsive force. The following picture illustrates the RPM algorithm:
Figure 1: RPM as a mapping algorithm.
In the initial RMP paper, the distance dij is defined as the minimal geodesic distance on the torus surface. This definition leads to a problem that, when two particles are located close to the opposite sites of the torus, the repulsive force between them becomes unstable with alternating directions. The following diagram illustrates this case (where I made the thickness of the torus infinitely small so that the torus becomes in effect a ring):
Figure 2: RPM dynamics anomaly on a ring: the force from A to B+ and B_ have different direction even B+ and B_ can be arbitrarily close to B.
In above diagram, the repulsive force between A and B can quickly change the direction when the particle B moves from position B_ to B+, because the repulsive force follows the minimal path that changed from upper half arc to lower half arc. As will be shown latter, this kind of discontinuity can lead to unwanted artifacts in the resulting RPM maps.
Formally, let's represent the ring by the numbers in the interval [0, w], where w is the length of the ring; let i and j be two data points mapped to the position x and y in [0, w]. With this representation the two ending points at 0 and w, as shown in the following picture, should be considered as stuck together:
Figure 3: Interval representation of a ring topology.
The energy and force between i and j according gRPM will be:
We can easily verify that Fij, as a function of x and y, is not continues when |x-y|=w/2. But, F*ij is continues and has the value 0 when |x-y|=w/2.
For two dimensional torus, there will be 4 different paths connecting any two different points on the torus surface. The four paths are illustrated in the following picture:
 |
Figure 4: Four paths between two points on a flat torus. Opposite edge of the rectangle should be consided stuck together.
Let (x0, x1) and (y0, y1) be the coordinate of two data points i and j, d0:=|x0-y0|, d1:=|x1-y1|; then the energy and force between the two points are:
To compare gRPM with RPM we have applied both algorithms to the sphere data set. The following pictures show the result:
Figure 5: Mapping 1000 data points sampled from a sphere surface to the flat torus: a) The original dataset displayed as scatter plot in the 3D sphace. b) The map generated by the RPM algorithm. c) The map generated by the gRPM algorithm.
We notice that there is kind of framing effect in the map generated by RPM algorithm: high concentration of data points along the boundary of the two square fragments. The map generated by gRPM does not suffer from such framing effect.
The key technique to move RPM to gRPM is to find a set of "conjugated" paths, so the forces induced by them will cancel each out at those "discontinuous" configurations of RPM. With this technique we have worked out gRPM algorithm for other relatively simple spaces (e.g. 2D smooth manifolds). In VisuMap we have implemented gRPM for flat klein-bottle, flat sphere, flat real projective plane (all flat fundamental polygons), 3D sphere and the projective plane in half-sphere model. The set of conjugated paths for these manifolds comprise 2 to 8 paths.
Discussions:
- The initial RPM algorithm defines the energy as 1/dpij, where p is any positive number. Just for the sake of simplicity, we have here just considered the case p=0. The handling of other values for p should be analogous. In fact, for any smooth monotonously increasing function h(x), we can use the function 1/h( dij) as energy function for gRPM.
- Notice that, for the ring topology, the two "conjugated" paths form a complete winding loop (see Figure 1.) As an extension, we could require that the path pair forms two winding loops. As shown in the following diagram, two particles will have minimal energy when they are at the same spot (that is the same phase but different loop). Thus, the repulsive force will be effectively turned into attractive force.

In general, we can easily verify that, for the ring topology, the interaction is repulsive when the path pair forms odd number of loops; and is attractive when the path pair forms even number of loops. This kind of winding number resemble the spin numbers of bosons and fermions in particle physics. It might be interesting to investigate gRPM for these more general cases.
- Visualization of high-dimensional data with relational perspective map, James X. Li, Information Visualization 2004; 3, 49-59.









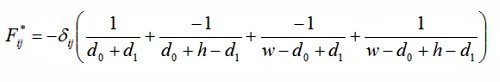

No comments:
Post a Comment