Transformation between rectangle and torus

I have found today a nice video clip from YouTube that visualizes the transformation between rectangle and torus surface. Torus surface is the base information space used by relational perspective map (RPM). This is main characteristics of RPM that distinguish RPM from other conventional mapping methods which use open Euclidean space as image space.

There is also good clips showing the construction of Klein-Bottle. But I could not find a good clip for the construction of real projective space. In order to visualize projective space and other more complex 2/3-D manifolds we probably need to partition the objects in some intuitive way.

New paper comparing CCA and Manifold learning arlgorithms

The journal Information Visualization has recently published a very interesting paper of J. Venna and S. Kaski with the title "Comparison of Visualization methods for an atlas of gene expression data sets".

This paper has compared the performance of many algorithms for mapping various kind of data sets. Algorithms considered include: PCA, LLE, Laplacian Eigenmap, Isomap and CCA. The performance comparison are done with diagram of trustworthiness and continuity which visualize, like Shepard diagram, the discrepancies between input- and output-distance matrices.

The advantage of the trustworthiness and continuity diagrams over the Shepard diagram is that they aggregate the discrepancy information uniformly over all data points, so that you get a single curve to show the quality of a map. With Shepard diagram you get a curve for each data point. Thus, trustworthiness/continuity diagrams are much easier to apply in practice. On the other side, the Shepard diagram provides more detailed information that allows, for instance, users to investigate mapping quality with respect to individual data points (not just the whole map).

Whereas those diagrams provide objective measures for mapping quality, I think they should be used with care. They may not always reflect the subjective mapping quality perceived by human, and the ultimately goal should be helping people not machines. Blindly trusting these numbers might discourage development of new useful algorithms. One main problem with these diagrams is, for instance, they don't have the concept of partition. Algorithms (like RPM) which simplify data by partitioning (apart from dimensionality reduction) are greatly penalized. Partition, as a perception method, is probably as fundamentally as focusing-by-proximity.

A main message of this paper is that CCA algorithm clearly and significantly out-performed other algorithms based on explicit unfolding. Our experience supports this assessment. We have not encountered a single data set that CCA performed noticeably worse than algorithms like LLE and Isomap. Sammon map and PCA cannot be compared directly with CCA as they preserve long distance information and visualize the over-all structure of the data set (instead of unfolding no-linear structure).

Symmetry between dimensionality reduction and data clustering

Dimensionality reduction and data clustering are two main types of services offered by VisuMap to support visual exploration of high dimensional data. Although there was no explicit plan in the initial design of VisuMap to develop these two types of services in parallel, they have evolved nicely together in the software architecture.

We might argue that the reason for the nice coexistence are because they are both indispensable to explore high dimensional no-linear data. But there is another more profound reason for this: namely, they are conceptually symmetry to each other.

In order to see this "symmetry" let us consider a high dimensional dataset as a data table with rows and columns. The number of columns is normally also considered as the dimension of the data. A dimensionality reduction method basically tries to reduce the number of columns without losing much relevant information. On the other side, a clustering algorithm tries to group similar rows together so that the clusters preserve as much as possible information. In other words, the purpose of clustering algorithm is to reduce the number rows by replacing them with clusters.

In terms of "symmetry" we can say, dimensionality reduction algorithms reduce the number of columns whereas clustering algorithms reduce the number rows.

So, what does this symmetry brings us? One application of this symmetry is that we can transfer any clustering algorithm to a dimensionality reduction method (and vice versa) by transposing the data table as a matrix. For instance, we can apply a clustering method on the columns of dataset to get three clusters and use the centroids of the clusters as 3D coordinates for the rows. By doing so we reduce the dataset's dimension to 3.

The null-dataset

When we analyze a high dimensional dataset the first question is often:

Does the dataset contain useful information at all?

A simple way to answer this questions is as follows: We first construct a so called null-dataset that contains 100 data points; each data point is a 100 dimensional row vector of the following table:

1, 0, 0, ..., 0

0, 1, 0, ..., 0
0, 0, 1,...., 0

...

0, 0, 0,..., 1

Since the Euclidean distance between any two points from the null-dataset is the constant sqrt(2), the distance matrix contains no information about the data points in the sense that the distance matrix does not single out any group of points with special meaning.

Now for a new high dimensional dataset, we can simply apply a collection of MDS mapping methods to the dataset and to the null-dataset with the same configuration settings. If the MDS maps of the new dataset resemble those of the null-dataset, we can expect that the new dataset contains no meaningful information.

The following pictures show the 2D MDS maps of the null-dataset with 100 data points created with 4 MDS algorithms (i.e. RPM, Sammon, CCA and SMACOF) available in VisuMap:

We notice that three of these MDS algorithms resulted in similar disk alike maps, whereas the RPM algorithm produced a homogeneously distributed map (the first map).

In order to understand the behavior of MDS algorithms it is helpful to see how they react to injection of information by means of broken symmetry between the data points. For this purpose I have altered the null-dataset slightly be multiplying the vector of the first data point by the factor 1.05. This change singles out the first data point as it has slightly larger distance to other points. The following pictures are the corresponding MDS maps of dataset:

The first data point is shown as a red spot in above pictures. We can see that 3 of our MDS algorithms singled out the first point as an out-lier, whereas the RPM method ignored such alteration in the dataset. Similarly, we can alter the null-dataset by multiplying a factor 0.95 to the first data point. The following pictures show the corresponding MDS maps:

We can see that all 4 MDS mapping algorithms singled the first data point by moving it to the center of these maps.

In order to test our method for a real dataset I have created a dataset with ca. 500 data points. Each data point contains 100 daily price changes in percentage. The following pictures show its MDS maps created with the same set of configuration settings used for the null-dataset:

We can notice, more or less, some resemblance between above pictures and those of the null-dataset. This means, that the distance matrix probably doesn't carry much information about the stocks; and we probably won't be able to extract much information from the dataset using methods based on Euclidean distance. For example, it won't make sense to apply k-mean clustering or neural network algorithms directly on this dataset.

It should be pointed out here that above statments only apply to the Euclidean distance. If we use other distance metric to measure to distance between the data points (for instance use the correlation as a kind of distance) we might be able to extract useful information.

In general, the null-dataset method described above only applies to Euclidean distance. If we explore the dataset as a non-euclidean space, we need to adapt the null-dataset to that non-euclidean space.

VisFinance 1.2 Released

We have just released VisFinance 1.2.
VisFinance is a plugin module for VisuMap to provide
specialized services for finance data analysis.

Free trial version of VisFinance 1.2 can be downloaded at here.

VisuMap 2.5 Released.

Today we have released VisuMap version 2.5. This version has undergone major extensions and changes in scripting & pluging interfaces in order to accommodate more advanced plugin applications (e. g. the upcoming VisFinance plugin for finance service).

In this release we have not changed the formats of data files nor the configuration file, but plugins and scripts developed for version 2.4 or older might need to be upgraded to the new interface.

This release also includes many bug fixes, enhancements in user interfaces and performance. For instance, double-mouse-clicking has now been consistently linked to the task to switch the mode of a window. In the main window, double-clicking the main map now switches the main map between editing and shifting mode, instead of starting the RPM mapping algorithm as in the previous version.

In general, data drilling features (i.e. PCA, Data Details and Diagram view) now work in a more consistent and integrated way. For instance, you can now create a new dataset for selected data in almost all views with few mouse clicks.

Also, we have a new price list for our products and services.

The symmetry between repulsive and attractive force

The relational perspective map (RPM) algorithm in its core simulates a multi-particle system on a torus surface in which the particles exerts repulsive forces to each other. Some people has asked the question why just repulsive force? Why not use attractive forces like other force directed mapping methods?

A simple answer to this question is that we prefer to use a simpler dynamic system if it can solve the problem. Just like physicists who try to reduce the number of fundamental interactions, I would prefer to avoid using attractive force if it is not absolutely needed.

Classical multidimensional scaling (MDS) methods have to use both types of forces (as can be derived from their stress function) because their base information space is the infinite open Euclidean space: without attractive force their configuration will quickly degrade to infinite size; and without repulsive forces their configuration will shrink to a single point. With RPM method, the closed manifold (i.e. the torus surface) confines the configuration into a limited size.

Another not-so-obvious answer to above question is that on a closed manifold the repulsive and attractive forces are the manifestation of the same thing, from certain point of view at least. To see this, let use consider the simplest case of 1-dimensional curled space (i.e. the circle). As be shown in the following picture, imaging that we have two ants living on the circle and there are two positively charged particles on the circle which can move freely on the circle but are confined on the circle.

From the point of view of the ant on the left side, the two charges exert repulsive force to each other according to coulomb's law.

However, from the point of view of the ant on the right side, the two charges attract each other. This is a little contra-intuitive for us as observers from the 3-dimensional space. But, we need to remind us that these ants are living in the 1-dimensional space. The ant on the right side has no way to see the two charges moving apart from each other. This ant can only move on the circle, particularly the right arc of the circle, to measure the distance between the two charges. What this ant would find out is that the same force as indicated in the picture will seemly press the two charge closer to each other; and larger the charge, the stronger the force. Thus, the ant on the right side would claim that two charges attract each other according a law similar to the coulomb's law (the anti-coulomb's law?).

RPM, Curled Space and Dimensionality Reduction

The Relational Perspective Map (RPM) uses finite curled spaces as information space to map high dimension data. The curled space has caused some uneasiness for users without related background. In this blog I will explain a little about the curled spaces and describe an advantage of the curled spaces over the normal (infinite) Euclidean space.

First, in order to understand the curled space let us compare the 1-dimensional curled space with the 1-dimensional Euclidean space. The 1-dimensional Euclidean space (denoted as R) comprises all real numerical values from negative infinite to positive infinite. Graphically, the 1-dimensional Euclidean space can be depicted by a straight line that extends in both directions to the infinite as be shown by the first map in the following picture.



The curled 1-dimensional space, denoted as T, is graphically equivalent to a circle with a finite size as show in the middle map in above picture. To illustrate the difference between R and T it would be helpful to image an ant living in the spaces. An ant living in R, can walk in both directions indefinitely without coming back to the same spot. An ant living in T can also walk in both directions indefinitely, but it will come back to the same spot after a finite time of walking.

The curled space T can also represented as a segment of R of a finite length, say w, as be shown in the right map in above picture. In this representation, the begin and the end of the segment has to be considered as stuck together. That means, an imaginative ant walking on the segment can somehow be beamed from one end to anther end in no time. Analytically, T is represented by an interval [0, w]. The distance between two points a and b in T has to be defined differently as in R, though. One simple definition for the distance between two points a and b in T is as follows:

d(a, b) := min{|a-b|, w-|a-b|}

The analytically representation ([0,w], d) of T has the advantage over the graphical representation that it can be easily extended to high dimensional cases as we will see below.

The two dimensional curled space T² is graphically equivalent to the surface of a torus as depicted in the left map of the following picture. The torus surface can also be understood as the trace of a circle (i.e. T) moving along another circle. Analogously, we can represent the T² as rectangle of the width w and height h embedded in the 2-dimensional Euclidean space R² as depicted in the right map of the following picture.


The distance calculation on T² becomes somewhat more complicated. If we define the distance based on the first graphical representation, we would have to use path integral in the R³ which is certainly not trivial. Based on the second representation (as shown in the right map of the picture above) we can have a much simple distance function as follows:

d((x₁,y₁), (x₂,y₂)) := min{|x₂-x₁|, w-|x₂-x₁|} + min{|y₂-y₁|, h-|y₂-y₁|}

This distance function is equivalent to any other valid distance function on T² in the sense that two closely located points with respect to this distance function will also be close to each other with respect to any other valid distance function. This distance can be explained with an imaginative ant on the rectangle as follows: If we assume that the ant can only walk horizontally or vertically, and it can be beamed from any edge to its opposite edge in no time, Then the distance between two points a and b is the shortest walking distance for our ant to walk from a to b.

The 3-dimensional curled dimension T³ cannot be represented as a subspace of R³, but it can represented as a cubic whose opposite planes are identified with each other as depicted in the following picture:

The distance function on T³ can be defined analogously as on T² which we will omit here.
After explained the curled dimension we can now talk about the dimensionality reduction (DR). In general, DR means to squeeze data from high dimensional spaces into lower dimensional spaces. The lower dimensional representation of high dimensional data allows us to study the data by means of visualization, but the cost for DR is that we will lose some information which are present in the original high dimensional space.

One main challenge for DR algorithms is to preserve as much as possible relevant information. In order to do so, most DR methods define some kind of stress function that measures information lost of the lower dimensional representation. In this way, a DR algorithm is converted to an optimization algorithm that minimizes the stress function.

For any no-trivial minimization problem we all know that local minimum is a problem, and there more we squeeze the data, the worse the problem. One typical strategy to avoid local minimum is to introduce some kind of global permutation or variation, that doesn't always reduces the stress function, but might bridge us to a global minimum at the end. Genetic algorithm and simulated annealing, for instance, employ such strategy. The RPM algorithm also implicitly employs global strategy by using very large learning speed that vanishes gradually like the temperature in simulated annealing algorithm.

RPM algorithm also offers another strategy to avoid local minimum because of its use of curled finite dimensions. As mentioned above, there more we squeeze our data, the worse the local minimum problem will become. This also means that we can alleviate the local minimum problem by gradually squeeze data from high dimensional space to lower dimensional space.

More particularly, to create a 2-dimensional map for a dataset we can first map it first to 3-dimensional torus T³, then gradually reduces its height and ultimately change it to a 2-dimensional torus T² as depicted in the following picture:

The gradual dimensionality reduction is possible because the dimensions have finite size, so that we can change a dimension's size gradually to zero to effectively remove the dimension. In other words, we change our information space from dimension 3 to dimension 2.9, 2.8, 2.7, ... till 2.0. The partial dimension reflects the reduced size of the a selected curled dimension. More generally, we can use the same method to squezze a map from any high dimension space, dimension by dimension, into lower dimensional space.
With VisuMap software we can automated the gradual DR with a script. The following picture shows how RPM algorithm gradually squeezes a spherical dataset from T³ to T². In this way, we can expect that the 2-dimensional map is much closer to the global minimum.

VisuMap and Google Earth

I have been a frequent user of Google Earth. It is really amazing to visit interesting places all over the world. However, the way Google Earth implemented the mouse navigation has caused me a little concern for some time.

With Google Earth (with default settings of 4.0.2091 or older) you zoom into a location by scrolling the mouse wheel forewards which gives you the feeling of move yourself closer to earth. I could not get used to this behavior. When I wanted to zoom in, I often made the mistake to scroll the mouse wheel in opposite direction. In VisuMap software we have several views that simulated the 3D space navigation that allows the user to explore data like flying within the data. After some consideration we have decided to implement the zoom-in navigation contrarily to Google Earth default method, we zoom in closer to data by scrolling the mouse wheel backwards.

For quite long time we have thought to change our navigation method to the one like Google Earth, since we don't want to spoil our user's experience. Google Earth is such a popular software, there must be a reason that they implemented the navigation method that way, we though.

To my great relief today, when I upgraded my Google Earth to version 4.0.2737, the first thing I noticed is that Google Earth changed its default zoom-in method to the way we always though is the better way and implemented in our software.

In retrospect, I guess Google Earth first wanted to simulate flying an airplane around. Most people would probably have thought so too. If you were flying an airplane with the mouse, you probably tend to scroll back to pull the airplane.(e.g. to zoom-out from the image). However, most people are not used to the experience of flying an airplane. We tend rather to use the mouse to control the object (i.e. the earth) before us. Thus, the new Google Earth version has followed the common experience. I have great respect for Google's engineers for making such small yet relevant change. This remind me of some countries which still drive on the left lane, I would be scared to drive on the left lane.

New VisuMap Release

We have finally released VisuMap version 2.4.754 today. In this and several previous minor releases we have made major effort to re-structure and optimize the software to accoommand extermely large datasets. The software can now directly load datasets with upto 10000 data columns and show them as tables, diagrams and maps!

Standard GUI controls of .NET library (like DataGridView) can only support table upto 1000 columns. For tables with more than 5000 columns the user interface becomes practially unusable. So we have implemented explicite paging mechanism (which we call column band) that allows user to select a subset of columns for processing.

Interestingly the DataGridView has no performance issues with large number of rows (e.g. > 20000 rows).

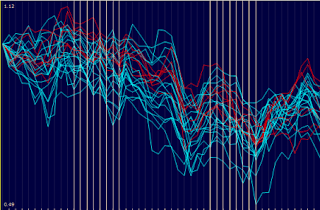
Another major addition to the software is the introduction of attribute mode for several views, like the details table and value diagrams. Up to now, VisuMap has mainly focused on exploration from the perspective of the object domain, so that users can easily select and explorer sub sets of bodies (or data rows). With the attribute mode, we have drastically simplified the investigation in the attributes domain (e.g. data columns). For instance, a user can select a subset of attributes by the mouse button, then create PCA projection of the selected attributes.

For example, the following value diagram shows the price history of some stocks. If we are interested in correlation between these stocks during the two major market down-turn periods, we can simply select these two periods and open the 3D PCA projection window for the selected attributes.