This video uses some features in VisuMap available in VisuMap version 3.2.855. The sample datasets used in the video are included in the standard installation of VisuMap.
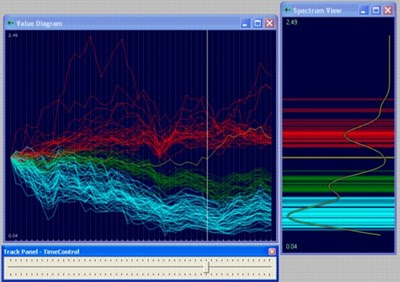

var randomWalk = New.NumberTable(500,50);The last line in above code block creates the following diagram (the diagram has been colored with k-mean algorithm):
for(var row=0; row < randomWalk.Rows; row++) {
var v = 1.0;
for( var col=0; col < randomWalk.Columns; col++) {
randomWalk.Matrix[row][col] = v;
v *= 1 + 0.01*(Math.random() - 0.5);
}
}
randomWalk.ShowValueDiagram();

| I1 | I2 | I3 | ... | Ik | |
| SNPa | T/T | G/T | T/T | ... | G/G |
| SNPb | C/T | C/C | C/T | ... | T/T |
| I1 | I2 | I3 | ... | Ik | |
| SNPa | 2 | 1 | 2 | ... | 0 |
| SNPb | 1 | 2 | 1 | ... | 0 |
The Sample Dataset
The uploaded sample dataset is obtained from the HapMap Project website that provides accesses to a large collection of genotype datasets. More interestingly, from that website we can select genotype data for special SNPs and populations. To generate the sample dataset I have select all SNPs from the region of the first 2 Million base pairs in the 9-th chromosome for the CEU population that consists of 169 individuals. There are altogether 1900 SNPs in the selected region. Our sample dataset is thus basically a table with 1900x169 nucleotide pairs.
In order to import the downloaded data into VisuMap we have implemented a plugin module HaploExplorer that enables users to import data downloaded from the HapMap website (files must have the extension .hmap.) The HaploExplorer plugin also implements a special metric named "LD R-Sqaured", so that users can simply select this metric to generate maps to visualize LD values. The following picture shows a sphere map of the 1900 SNPs:
In above map, each glyph represents a SNP from the dataset. The size of the glyph indicates the chromosome location of the SNP, ie. smaller glyphs represent SNPs located at the beginning of the chromosome. Most importantly, the distances between the glyphs indicate the LD between the SNPs; that means closely located glyphs correspond to SNPs with high LD. We can see clearly various type of clusters in above picture.
We can also visualize the chromosome locations more directly with the help a spectrum view. The following picture shows, for instance, a 2D-RPM map of the the dataset together with a spectrum view of their chromosome locations:
When interactively exploring about views, the user can select a group of SNPs in the lower window, the upper spectrum window will automatically show the chromosome locations of the selected SNPs.
For comparison purpose the HapMap project recommends a program called Haploview that allows user to directly visualize LD values with a triangle matrix, where the LD values are represented by different levels of gray colors. The following picture shows such a map generated by Haploview:
Comparing above maps, we can see that VisuMap provides a more direct and intuitive way to visualize patterns among SNPs. More importantly, as an integrated software package, VisuMap offers simple framework to investigate different type of LD relationships between SNPs. We can, for instance, easily experiment with any other comparable distance metric available in VisuMap; and we can use any of clustering algorithms in VisuMap to cluster the SNPs.
At last, but not at least, after we have imported the data in to VisuMap, we can also visualize patterns among populations by transposing the dataset table. In order to study relationships between individuals or populations a special distance metric, called the IBS (identity-by-state) distance, has been suggested by some researchers. The IBS distance metric is also implemented in the HaploExplorer plugin. After we have transposed a SNP dataset, we can select the IBS distance metric to produce population maps.